(Trang 33)
1.27. Trong mặt phẳng toạ độ Oxy, cho đường thằng 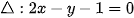 và hai điểm A(-1, 2), B(-3; 4).
và hai điểm A(-1, 2), B(-3; 4).
a) Tìm toạ độ điềm A' là ảnh của điểm A qua phép đối xứng trục  .
.
b) Xác định điểm M thuộc đường thẳng  sao cho MA+ MB đạt giá trị nhỏ nhất.
sao cho MA+ MB đạt giá trị nhỏ nhất.
1.28. Trong mặt phằng toạ độ Oxy, cho đường thằng d: 2x - y + 5=0. Viết phương trình đường thẳng d' là ảnh của đường thằng d qua phép tịnh tiến theo vecto 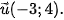
1.29. Trong mặt phẳng toạ độ Oxy, cho đường tròn (C): x2 + y2 - 2x - 4y - 4=0. Viết phương trình của đường tròn (C') là ảnh của đường tròn (C) qua phép đối xứng tâm A(3;-3).
1.30. Trong mặt phẳng toa độ Oxy, cho đường tròn (C): (x - 1)2 + (y + 2)2 = 9. Phép vị tự tâm O(0;0) với tỉ số k = -2 biến đường tròn (C) thành đường tròn (C'). Viết phương trình đường tròn (C').
1.31. Cho đường thẳng ở và hai điểm A, B cùng thuộc một nửa mặt phẳng bờ d. Hai điểm E, F thay đổi trên d sao cho 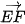 không đổi. Xác định vị trí của hai điểm E, F đề AE + BF nhỏ nhất.
không đổi. Xác định vị trí của hai điểm E, F đề AE + BF nhỏ nhất.
1.32. Cho tam giác ABC nội tiếp đường tròn tâm O. Các đỉnh B, C cố định còn đỉnh A thay đổi trên đường tròn đó. Vẽ hình bình hành ABCD. Chứng minh rằng điểm D luôn thuộC một đường tròn cố định.
1.33. Cho nửa đường tròn tâm O, đường kinh AB và điểm M trên nửa đường tròn đó. Dựng về phía ngoài của tam giác ABM tam giác AMN vuông cân tại M. Chứng minh rằng khi M thay đổi trên nửa đường tròn thì điểm N luôn thuộc một nửa đường tròn cố định.
1.34. Bằng quan sát và đo đạc, hãy cho biết hai hình sau (H.1.55) có đồng dạng với nhau hay không.


























