Trang 5
Chuyên đề này giới thiệu biến ngẫu nhiên rời rạc, công thức Bernoulli (mang tên nhà toán học người Thuỵ Sĩ Jacob Bernoulli) và biến ngẫu nhiên có phân bố nhị thức (gắn với công thức Bernoulli). Chuyên đề cũng nêu ứng dụng của các kiến thức trên vào một số bài toán có nội dung thực tiễn.

Jacob Bernoulli (1655-1705) (Ảnh: wikipedia)
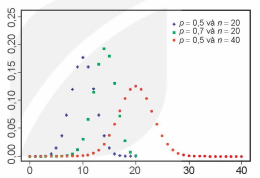
Biến ngẫu nhiên có phân bố nhị thức với tham số p và n
| THUẬT NGỮ | KIẾN THỨC, KĨ NĂNG |
| • Biến ngẫu nhiên rời rạc • Bảng phân bố xác suất của biến ngẫu nhiên rời rạc • Kì vọng, phương sai và độ lệch chuẩn của biến ngẫu nhiên rời rạc | Nhận biết khái niệm biến ngẫu nhiên rời rạc. Biết lập bảng phân bố xác suất của biến ngẫu nhiên rời rạc. Biết tính kì vọng, phương sai và độ lệch chuẩn của biến ngẫu nhiên rời rạc và giải thích ý nghĩa của chúng. |
Trong một trò chơi, các câu hỏi gồm hai loại I và II:
• Với câu hỏi loại I: Trả lời đúng được 20 điểm. Trả lời sai không được điểm (0 điểm).
•Với câu hỏi loại II: Trả lời đúng được 80 điểm. Trả lời sai không được điểm (0 điểm).
Trang 6
Ở vòng 1, người chơi được chọn một trong hai loại câu hỏi. Sau khi chọn xong loại câu hỏi, người chơi bốc thăm ngẫu nhiên một câu hỏi trong loại đó. Nếu trả lời sai thì phải dừng cuộc chơi. Nếu trả lời đúng, thí sinh sẽ bước vào vòng 2, bốc ngẫu nhiên một câu hỏi trong loại còn lại. Người chơi trả lời đúng hay sai, cuộc chơi cũng kết thúc tại đây. Giả thiết rằng việc trả lời đúng câu hỏi vòng 1 sẽ không ảnh hưởng đến xác suất trả lời đúng hay sai câu hỏi ở vòng 2.
Bạn Minh tham gia cuộc chơi. Giả sử xác suất để Minh trả lời đúng câu hỏi loại I là 0,8; xác suất để Minh trả lời đúng câu hỏi loại II là 0,6.
Hỏi ở vòng 1 Minh nên chọn câu hỏi loại I hay câu hỏi loại II?
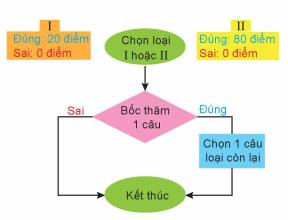
Hình 1.1
(I) Đúng: 20 điểm
Sai: 0 điểm
(II) Đúng: 80 điểm
Sai: 0 điểm
Chọn loại I hoặc II
Bốc thăm 1 câu
Đúng
Chọn 1 câu loại còn lại
Sai
Kết thúc
1. BIẾN NGẪU NHIÊN RỜI RẠC VÀ BẢNG PHÂN BỐ XÁC SUẤT CỦA NÓ
HĐ1. Hình thành khái niệm biến ngẫu nhiên rời rạc
Gieo một xúc xắc cân đối, đồng chất liên tiếp 6 lần. Gọi X là số lần xúc xắc xuất hiện mặt 6 chấm trong 6 lần gieo liên tiếp đó.
a) Các giá trị có thể của X là gì?
b) Trước khi thực hiện việc gieo xúc xắc đó, ta có khẳng định trước được X sẽ nhận giá trị nào không?
Đại lượng X được gọi là một biến ngẫu nhiên rời rạc nếu nó nhận một số hữu hạn các giá trị có thể. Các giá trị đó là các số và không dự đoán được trước khi phép thử được thực hiện.
Ví dụ 1. Tung một đồng xu cân đối, đồng chất liên tiếp 3 lần. Gọi X là số lần đồng xu xuất hiện mặt ngửa.
a) X có là một biến ngẫu nhiên rời rạc hay không?
b) Liệt kê các giá trị có thể của X và tính các xác suất để X nhận các giá trị đó.
Giải
a) Vì X chỉ nhận một số hữu hạn giá trị là 0, 1, 2, 3 và không dự đoán trước được khi tung đồng xu nên X là một biến ngẫu nhiên rời rạc.
b) Các giá trị có thể của biến ngẫu nhiên rời rạc X là một số thuộc tập A = {0; 1; 2; 3}. Ta phải tính các xác suất P(X = 0); P(X = 1); P(X = 2); P(X = 3), trong đó:
P(X = 0) là xác suất để không có lần xuất hiện mặt ngửa;
P(X = 1) là xác suất để có đúng 1 lần xuất hiện mặt ngửa;
P(X = 2) là xác suất để có đúng 2 lần xuất hiện mặt ngửa;
P(X = 3) là xác suất để cả ba lần đều xuất hiện mặt ngửa.
Không gian mẫu Ω = {SSN; SNN; NSN; NNN; SSS; SNS; NSS; NNS}, n(Ω) = 8.
Biến cố {X = 0} là biến cố: “Không có lần nào xuất hiện mặt ngửa".
{X = 0 } là tập {SSS} có 1 phần tử. Vậy 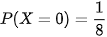 .
.
Trang 7
Biến cố {X = 1} là biến cố: “Có đúng 1 lần xuất hiện mặt ngửa”.
{X = 1} là tập {SSN; SNS; NSS} có 3 phần tử. Vậy 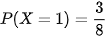 .
.
Biến cố {X = 2} là biến cố: “Có đúng 2 lần xuất hiện mặt ngửa”.
{X = 2} là tập {SNN; NSN; NNS} có 3 phần tử. Vậy 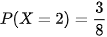 .
.
Biến cố {X = 3} là biến cố: “Cả ba lần xuất hiện mặt ngửa”.
{X = 3} là tập {NNN} có 1 phần tử. Vậy 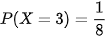 .
.
| Giả sử X là một biến ngẫu nhiên rời rạc nhận các giá trị
|
HĐ2. Cùng cố khái niệm bảng phân bố xác suất của biến ngẫu nhiên rời rạc
Hãy nêu số thích hợp với dấu "?" để hoàn thành bảng phân bố xác suất của biến ngẫu nhiên rời rạc X trong Ví dụ 1.
| X | 0 | 1 | 2 | 3 |
| P | ? | ? | ? | ? |
Trong bảng phân bố xác suất của biến ngẫu nhiên rời rạc X, ta có: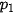 + + 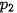 + ... + + ... + 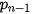 + + 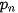 = 1. = 1. |
Ví dụ 2. Cho biến ngẫu nhiên rời rạc X với bảng phân bố xác suất như sau:
| X | 0 | 1 | 2 | 3 |
| P | a | a | 3a | 3a |
Tìm a.
Giải
Ta có a + a + 3a + 3a = 1. Suy ra 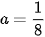 .
.
Ví dụ 3. Giả sử số vụ vi phạm Luật Giao thông trên một đoạn đường vào tối thứ Bảy là một biến ngẫu nhiên rời rạc X với bảng phân bố xác suất như sau:
| X | 0 | 1 | 2 | 3 | 4 | 5 |
| P | 0,1 | 0,2 | 0,3 | 0,2 | 0,15 | 0,05 |
Tính xác suất để tối thứ Bảy:
a) Xảy ra nhiều nhất 1 vụ vi phạm Luật Giao thông;
b) Xảy ra ít nhất 3 vụ vi phạm Luật Giao thông;
c) Xảy ra ít nhất 2 vụ vi phạm Luật Giao thông.
Trang 8
Giải
a) Gọi A là biến cố: “Xảy ra nhiều nhất 1 vụ vi phạm Luật Giao thông vào tối thứ Bảy”. Khi đó, A là hợp của hai biến cố xung khắc: {X = 0} và {X = 1}. Tức là A = {X = 0} ∪ {X = 1}. Theo quy tắc cộng xác suất, ta có:
P(A) = P(X = 0) + P(X = 1) = 0,1 + 0,2 = 0,3.
b) Gọi B là biến cố: “Xảy ra ít nhất 3 vụ vi phạm Luật Giao thông vào tối thứ Bảy";
C là biến cố: “Xảy ra 4 hoặc 5 vụ vi phạm Luật Giao thông vào tối thứ Bảy”.
Khi đó, B là hợp của hai biến cố xung khắc: biến cố {X = 3} và biến cố C. Theo quy tắc cộng xác suất, ta có:
P(B) = P(X = 3) + P(C).
Biến cố C là hợp của hai biến cố xung khắc: (X = 4} và {X = 5}. Theo quy tắc cộng xác suất, ta có:
P(C) = P(X = 4) + P(X = 5).
Do đó
P(B) = P(X = 3) + P(C) = P(X = 3) + P(X = 4) + P(X = 5) = 0,2 + 0,15 + 0,05 = 0,4.
c) Gọi D là biến cố: “Xảy ra ít nhất 2 vụ vi phạm Luật Giao thông vào tối thứ Bảy”. Suy ra D là biến cố đối của biến cố A. Vậy P(D) = 1 – P(A) = 1 – 0,3 = 0,7.
Ví dụ 4. Một túi đựng 6 viên bi đỏ và 4 viên bị xanh. Các viên bị có cùng kích thước và khối lượng. Lấy ngẫu nhiên đồng thời 3 viên bi từ trong túi. Gọi X là số viên bị xanh trong 3 viên bi lấy ra. Lập bảng phân bố xác suất của X.
Giải
Các giá trị có thể của X thuộc tập {0; 1 2 3}.
Tiếp theo, ta cần tính P(X = 0), P(X = 1), P(X = 2), P(X = 3).
Số kết quả có thể là 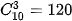 .
.
• Tính P(X =0): Biến cố {X = 0} là: “Lấy được 3 viên bi đỏ”.
Số kết quả thuận lợi cho biến cố {X =0} là 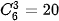 . Do đó
. Do đó 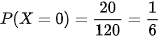 .
.
• Tính P(X = 1): Biến cố {X =1} là: "Lấy được 1 viên bị xanh và 2 viên bi đỏ".
Có 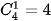 cách chọn 1 viên bi xanh trong 4 viên bi xanh và
cách chọn 1 viên bi xanh trong 4 viên bi xanh và 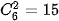 cách chọn 2 viên bi đỏ trong 6 viên bị đỏ.
cách chọn 2 viên bi đỏ trong 6 viên bị đỏ.
Theo quy tắc nhân ta có 4 · 15 = 60 cách chọn 1 viên bi xanh và 2 viên bi đỏ.
Số kết quả thuận lợi cho biến cố {X = 1} là 60. Do đó 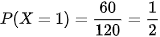 .
.
• Tính P(X = 2): Biến cố {X = 2} là: “Lấy được 2 viên bi xanh và 1 viên bi đỏ”.
Có 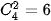 cách chọn 2 viên bi xanh trong 4 viên bi xanh và
cách chọn 2 viên bi xanh trong 4 viên bi xanh và 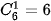 cách chọn 1 viên bi đỏ trong 6 viên bị đỏ.
cách chọn 1 viên bi đỏ trong 6 viên bị đỏ.
Theo quy tắc nhân ta có 6 · 6 = 36 cách chọn 2 viên bi xanh và 1 viên bị đỏ. Số kết quả thuận lợi cho biến cố {X = 2} là 36. Do đó 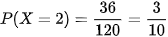 .
.
• Tính P(X = 3): Biến cố {X = 3} là: “Lấy được 3 viên bi xanh". Số kết quả thuận lợi cho biến cố {X = 3} là 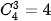 . Do đó
. Do đó 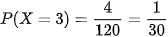 .
.
Trang 9
Bảng phân bố xác suất của X là:
| X | 0 | 1 | 2 | 3 |
| P | 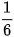 | 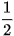 | 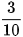 | 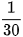 |
Luyện tập 1. Một tổ có 10 học sinh nam và 6 học sinh nữ. Giáo viên chọn ngẫu nhiên đồng thời 3 học sinh. Gọi X là số học sinh nam trong 3 học sinh được chọn. Lập bảng phân bố xác suất của X.
Vận dụng 1. Một trò chơi sử dụng một hộp đựng 20 quả cầu có kích thước và khối lượng như nhau được ghi số từ 1 đến 20. Người chơi lấy ngẫu nhiên đồng thời 3 quả cầu trong hộp. Gọi X là số lớn nhất ghi trên 3 quả cầu đã lấy ra.
a) Lập bảng phân bố xác suất của X.
b) Người chơi thắng cuộc nếu trong 3 quả cầu lấy ra có ít nhất 1 quả cầu ghi số lớn hơn 18. Tính xác suất thắng của người chơi.
Hướng dẫn
a) Tập các giá trị có thể của X là {3; 4;...; 20}. Ta tính P(X = k), với k ∈ {3; 4; ...; 20}.
Số kết quả có thể là 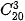 = 1 140.
= 1 140.
Biến cố {X = k} là biến cố: "Trong 3 quả cầu lấy ra có một quả cầu đánh số k và 2 quả cầu đánh số nhỏ hơn k". Số kết quả thuận lợi là 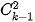
Vậy 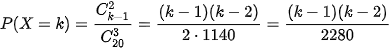 .
.
b) Biến cố “Người chơi thắng" là biến cố hợp của hai biến cố {X = 19} và {X = 20}.
2. CÁC SỐ ĐẶC TRƯNG CỦA BIẾN NGẪU NHIÊN RỜI RẠC
a) Kì vọng
HĐ3. Hình thành khái niệm kì vọng
Giả sử số vụ vi phạm Luật Giao thông trên một đoạn đường AB trong 98 buổi tối thứ Bảy được thống kê như sau: 10 tối không có vụ nào; 20 tối có 1 vụ; 23 tối có 2 vụ; 25 tối có 3 vụ; 15 tối có 4 vụ; 5 tối có 7 vụ. Hỏi trung bình có bao nhiêu vụ vi phạm Luật Giao thông trên đoạn đường AB trong 98 buổi tối thứ Bảy đó?
Để có một ý niệm về độ lớn trung bình của biến ngẫu nhiên X ta có khái niệm kì vọng của X.
| Cho X là một biến ngẫu nhiên rời rạc với bảng phân bố xác suất
Kì vọng của X, kí hiệu là E(X), là một số được tính theo công thức sau: |
Trang 10
Nhận xét
• Kì vọng E(X) là một số cho ta một ý niệm về độ lớn trung bình của X nên kì vọng E(X) còn được gọi là giá trị trung bình của X.
• E(X) được tính thông qua bảng phân bố xác suất của X.
• E(X) không nhất thiết thuộc tập các giá trị có thể của X.
Ví dụ 5. Trong mỗi buổi ông An đi câu cá, ông có thể câu được 0; 1; 2; 3; 4 con cá với các xác suất tương ứng là 0,16; 0,17; 0,25; 0,28 và 0,13. Hỏi trung bình ông An câu được bao nhiêu cá trong một buổi đi câu?
Giải
Gọi X là số con cá ông An câu được trong một buổi câu.
Theo giả thiết X là biến ngẫu nhiên rời rạc có bảng phân bố xác suất như sau:
| X | 0 | 1 | 2 | 3 | 4 |
| P | 0,16 | 0,18 | 0,25 | 0,28 | 0,13 |
Ta có:
E(X) = 0 - 0,16 + 1 · 0,18 + 2 · 0,25 + 3 · 0,28 + 4 · 0,13 = 2,04.
Vậy trung bình ông An câu được 2,04 con cả trong một buổi đi câu.
Luyện tập 2. Giả sử số vụ vi phạm Luật Giao thông trên một đoạn đường vào tối thứ Bảy có thể là 0; 1; 2; 3; 4; 5 với các xác suất tương ứng là 0,1; 0,2; 0,25; 0,25; 0,15 và 0,05. Hỏi trung bình có bao nhiêu vụ vi phạm Luật Giao thông trên đoạn đường đó vào tối thứ Bảy?
Ví dụ 6. Trở lại tình huống mở đầu. Giả sử ở vòng 1 bạn Minh bốc ngẫu nhiên một câu hỏi loại I. Hỏi trung bình Minh nhận được bao nhiêu điểm?
Giải
Gọi X là số điểm Minh nhận được. Số điểm trung bình mà Minh nhận được là E(X).
Gọi A là biến cố: “Minh trả lời đúng câu hỏi loại I"; B là biến cố: “Minh trả lời đúng câu hỏi loại II”.
Ta có P(A) = 0,8; P(B) = 0,6.
• Vòng 1: Minh bốc ngẫu nhiên một câu hỏi loại I. Có hai khả năng:
Nếu trả lời sai thì Minh nhận 0 điểm. Cuộc chơi kết thúc tại đây. Ta có {X = 0} = 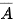 . Do đó
. Do đó
P(X = 0) = P(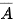 ) = 1 - P(A) = 1 - 0,8 = 0,2.
) = 1 - P(A) = 1 - 0,8 = 0,2.
Nếu trả lời đúng thì Minh nhận 20 điểm và Minh sẽ bước vào vòng 2.
• Vòng 2: Minh bốc ngẫu nhiên một câu hỏi loại II. Khi đó có hai khả năng:
+ Nếu trả lời sai, Minh không có điểm và phải dừng cuộc chơi với tổng số điểm nhận được là
20 + 0 = 20 (điểm).
Ta có {X = 20} = 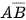 . Theo giả thiết A và B là hai biến cố độc lập nên A và
. Theo giả thiết A và B là hai biến cố độc lập nên A và 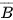 cũng độc lập. Theo công thức nhận xác suất cho hai biến cố độc lập ta có:
cũng độc lập. Theo công thức nhận xác suất cho hai biến cố độc lập ta có:
P(X = 20) = P(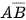 ) = P(A) · P(
) = P(A) · P(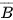 ) = 0,8 · (1 - 0,6) = 0,32.
) = 0,8 · (1 - 0,6) = 0,32.
+ Nếu trả lời đúng Minh nhận 80 điểm. Cuộc thi kết thúc tại đây và tổng số điểm Minh nhận được là
20 + 80 = 100 (điểm).
Ta có {X = 100} = AB. Theo giả thiết A và B là hai biến cố độc lập. Theo công thức nhân xác suất cho hai biến cố độc lập ta có:
P(X = 100) = P(AB) = P(A) · P(B) = 0,8 · 0,6 = 0,48.
Trang 11
Bảng phân bố xác suất của X:
| X | 0 | 20 | 100 |
| P | 0,2 | 0,32 | 0,48 |
Từ đó E(X) = 0 · 0,2 + 20 · 0,32 + 100 · 0,48 = 54,4.
Vậy trung bình Minh được 54,4 điểm.
Vận dụng 2. Tiếp tục xét tình huống mở đầu, giả sử ở vòng 1 Minh chọn câu hỏi loại II.
a) Hỏi trung bình Minh nhận được bao nhiêu điểm?
b) Ở vòng 1 Minh nên chọn loại câu hỏi nào?
Hướng dẫn
Gọi Y là số điểm Minh nhận được. Số điểm trung bình Minh nhận được là E(Y). Tương tự như Ví dụ 6, ta lập bảng phân bố xác suất của Y từ đó tính được E(Y).
Nếu E(Y) < E(X) thì ở vòng 1 Minh nên chọn câu hỏi loại I.
Nếu E(Y) > E(X) thì ở vòng 1 Minh nên chọn câu hỏi loại II.
b) Phương sai và độ lệch chuẩn
HĐ4. Hình thành khái niệm phương sai
Một nhà đầu tư xem xét hai phương án đầu tư. Với phương án 1 thì doanh thu một năm sẽ là 8 tỉ đồng hoặc 2 tỉ đồng với xác suất tương ứng là 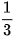 và
và 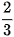 . Với phương án 2 thì doanh thu một năm sẽ là 5 tỉ đồng hoặc 3 tỉ đồng với hai xác suất bằng nhau.
. Với phương án 2 thì doanh thu một năm sẽ là 5 tỉ đồng hoặc 3 tỉ đồng với hai xác suất bằng nhau.
a) Hãy so sánh doanh thu trung bình của phương án 1 và phương án 2.
b) Nhà đầu tư nên chọn phương án nào?
Cho X là một biến ngẫu nhiên rời rạc. Để có một ý niệm về mức độ phân tán các giá trị của X xung quanh kì vọng E(X), ta có khái niệm phương sai và độ lệch chuẩn sau đây:
| Cho X là một biến ngẫu nhiên rời rạc với bảng phân bố xác suất như sau:
|
Câu hỏi
Trở lại HĐ4. Gọi X và Y tương ứng là doanh thu theo phương án 1 và phương án 2. Tính độ lệch chuẩn của X và Y.
Trang 12
Nhận xét
• V(X) còn có thể tính theo công thức sau:
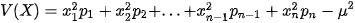 . (2)
. (2)
Công thức trên giúp ta tính V(X) nhanh hơn công thức (1) vì bớt đi được n phép trừ.
• Phương sai V(X) là một số không âm. Nó cho ta một ý niệm về mức độ phân tán các giá trị của X xung quanh kì vọng E(X). Phương sai càng lớn thì độ phân tán càng lớn.
• Cũng như phương sai, độ lệch chuẩn σ(X) cho ta một ý niệm về mức độ phân tán các giá trị của X xung quanh kì vọng E(X).
• Phương sai không có cùng đơn vị đo với X, còn độ lệch chuẩn có cùng đơn vị đo với X.
Ví dụ 7. Cho biến ngẫu nhiên rời rạc X với bảng phân bố xác suất:
| X | 0 | 1 | 2 | 3 | 4 | 5 |
| P | 0,1 | 0,2 | 0,3 | 0,2 | 0,1 | 0,1 |
a) Tính V(X) và σ(X) theo định nghĩa
b) Tính V(X) theo công thức (2).
Giải
a) Ta có
E(X) = 0 · 0,1 + 1 · 0,2 + 2 · 0,3 + 3 · 0,2 + 4 · 0,1 + 5 · 0,1 = 2,3.
Theo định nghĩa phương sai, ta có:
V(X) = (0 - 2,3)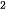 · 0,1 + (1 - 2,3)
· 0,1 + (1 - 2,3)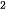 · 0,2 + (2 - 2,3)
· 0,2 + (2 - 2,3)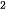 · 0,3 + (3 - 2,3)
· 0,3 + (3 - 2,3)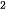 · 0,2 + (4 - 2,3)
· 0,2 + (4 - 2,3)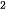 · 0,1 + (5 - 2,3)
· 0,1 + (5 - 2,3)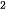 · 0,1 = 2,01.
· 0,1 = 2,01.
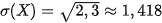 .
.
b) Theo công thức (2), ta có:
V(X) = 0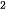 · 0,1 + 1
· 0,1 + 1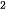 · 0,2 + 2
· 0,2 + 2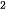 · 0,3 + 3
· 0,3 + 3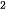 · 0,2 + 4
· 0,2 + 4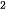 · 0,1 + 5
· 0,1 + 5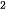 · 0,1 - 2,3
· 0,1 - 2,3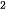 = 2,01.
= 2,01.
Luyện tập 3. Cho biến ngẫu nhiên rời rạc X với bảng phân bố xác suất như sau:
| X | 0 | 1 | 2 | 3 | 4 |
| P | 0,16 | 0,18 | 0,25 | 0,28 | 0,13 |
a) Tính V(X) và σ(X) theo định nghĩa.
b) Tính V(X) theo công thức (2).
Trang 13
BÀI TẬP
1.1. Giả sử số ca cấp cứu ở một bệnh viện vào tối thứ Bảy là một biến ngẫu nhiên rời rạc X có bảng phân bố xác suất như sau:
| X | 0 | 1 | 2 | 3 | 4 | 5 |
| P | 0,12 | 0,28 | 0,31 | 0,19 | 0,08 | 0,02 |
a) Tính xác suất để xảy ra ít nhất một ca cấp cứu ở bệnh viện đó vào tối thứ Bảy.
b) Biết rằng nếu có hơn 3 ca cấp cứu thì bệnh viện phải tăng cường thêm bác sĩ trực. Tính xác suất phải tăng cường bác sĩ trực vào tối thứ Bảy ở bệnh viện đó.
c) Tính E(X), V(X) và σ(X).
1.2. Số cuộc điện thoại gọi đến một trung tâm cứu hộ trong khoảng thời gian từ 12 giờ đến 13 giờ là một biến ngẫu nhiên rời rạc X có bảng phân bố xác suất như sau:
| X | 0 | 1 | 2 | 3 | 4 | 5 |
| P | 0,25 | 0,2 | 0,15 | 0,15 | 0,13 | 0,12 |
a) Tính xác suất để xảy ra ít nhất 2 cuộc gọi đến trung tâm cứu hộ đó.
b) Tính xác suất để xảy ra nhiều nhất 3 cuộc gọi đến trung tâm cứu hộ đó.
c) Tính E(X), V(X) và σ(X).
1.3. Một túi gồm các tấm thẻ giống hệt nhau chỉ khác màu, trong đó có 10 tấm thẻ màu đỏ và 6 tấm thẻ màu xanh. Rút ngẫu nhiên đồng thời ra 3 tấm thẻ từ trong túi.
a) Gọi X là số thẻ đỏ trong ba thẻ rút ra. Lập bảng phân bố xác suất của X. Tính E(X).
b) Giả sử rút mỗi tấm thẻ màu đỏ được 5 điểm và rút mỗi tấm thẻ màu xanh được 8 điểm. Gọi Y là số điểm thu được sau khi rút 3 tấm thẻ từ trong túi. Lập bảng phân bố xác suất của Y.
1.4. Hai xạ thủ An và Bình tập bắn một cách độc lập với nhau. Mỗi người thực hiện hai phát bắn một cách độc lập. Xác suất bắn trúng bia của An và của Bình trong mỗi phát bắn tương ứng là 0,4 và 0,5.
Gọi X là số phát bắn trúng bia của An, Y là số phát bắn trúng bia của Bình.
a) Lập bảng phân bố xác suất của X, Y.
b) Tính E(X), E(Y), V(X), V(M).
1.5. Trong một chiếc hộp có 10 quả cầu có kích thước và khối lượng giống nhau, trong đó có 4 quả ghi số 1; 3 quả ghi số 2; 2 quả ghi số 3 và 1 quả ghi số 4. Lấy ngẫu nhiên đồng thời hai quả cầu rồi cộng hai số trên hai quả cầu với nhau. Gọi X là kết quả thu được. Lập bảng phân bố xác suất của X.
Trang 14
Em có biết?
Biến ngẫu nhiên nhận một số vô hạn các giá trị có thể
Bạn Tùng gieo một con xúc xắc cân đối liên tiếp một cách độc lập cho đến khi nào xuất hiện mặt 6 chấm thì dừng lại. Gọi X là số lần gieo cần thiết để xuất hiện mặt 6 chấm. Các giá trị có thể của X là các số nguyên dương 1; 2; 3;... và không dự đoán trước được trước khi Tùng thực hiện việc gieo con xúc xắc. Như vậy X là một biến ngẫu nhiên nhận một số vô hạn các giá trị có thể.
Ta hãy tính P(X = k) (k ∈ N*) với {X = k} là biến cố: “k – 1 lần gieo đầu tiên không xuất hiện mặt 6 chấm và lần gieo thứ k xuất hiện mặt 6 chấm”.
Gọi 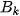 là biến cố: "k lần gieo đầu tiên không xuất hiện mặt 6 chấm”;
là biến cố: "k lần gieo đầu tiên không xuất hiện mặt 6 chấm”; 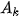 là biến cố: “Lần gieo thứ k xuất hiện mặt 6 chấm". Khi đó {X = k} =
là biến cố: “Lần gieo thứ k xuất hiện mặt 6 chấm". Khi đó {X = k} = 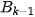
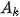 .
.
Theo công thức nhân xác suất: 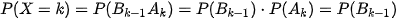 (1)
(1)
Ta chứng minh 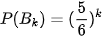 (2)
(2)
Chứng minh bằng quy nạp. Bước cơ sở: Với k = 1 công thức (2) hiển nhiên đúng.
Bước quy nạp: Giả sử khẳng định đúng với k. Ta phải chứng minh khẳng định đúng với k +1. Ta có 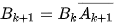 . Theo công thức nhận xác suất và giả thiết quy nạp suy ra
. Theo công thức nhận xác suất và giả thiết quy nạp suy ra
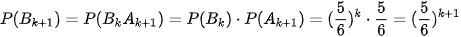 .
.
Vậy khẳng định đúng với k + 1. Theo nguyên lí quy nạp, (2) đúng với mọi k ∈ N*.
Từ (1) và (2) ta suy ra 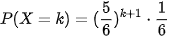
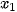 ,
, 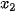 ,...,
,..., 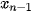 ,
, 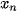 với các xác suất tương ứng là
với các xác suất tương ứng là 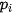 (i = 1, 2,..., n).
(i = 1, 2,..., n).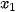
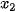
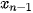
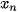
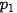
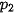
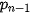
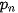
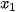
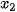
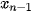
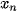
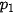
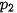
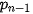
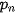
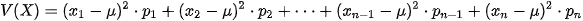 . (1)
. (1) 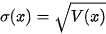 .
.
























