Trang 60
| THUẬT NGỮ • Đầu tư • Niên kim • Số tiền của niên kim | KIẾN THỨC, KĨ NĂNG • Thiết lập kế hoạch tài chính cá nhân cho các nhu cầu dài hạn như giáo dục hoặc sống tự lập. • Vận dụng kiến thức toán học trong việc giải quyết một số ván de ve dau tu. • Giá trị hiện tại của niên kim |

Anh Nam trúng giải xổ số độc đắc trị giá 5 tỉ đồng, và số tiền trúng thưởng này sẽ được trả dần 500 triệu mỗi năm trong vòng 10 năm. Tính giá trị hiện tại của số tiền trúng thưởng nếu anh Nam có thể tìm được một hình thức đầu tư với lãi suất kép 10% mỗi năm.
1. MỘT SỐ VẤN ĐỀ VỀ ĐẦU TƯ
Trong tài chính, đầu tư là một hoạt động sử dụng những nguồn lực ở hiện tại (gọi chung là vốn) như tiền bạc, vật chất, nhân công, trí tuệ, thời gian,... để đạt được lợi nhuận và lợi ích kinh tế lớn hơn trong tương lai so với nguồn lực đã bỏ ra.
Bất kì hình thức đầu tư sinh lợi nhuận nào cũng luôn đi cùng với rủi ro. Song mức độ rủi ro cao hay thấp, lợi nhuận ít hay nhiều sẽ phụ thuộc vào loại hình đầu tư lựa chọn.
Những kênh đầu tư phổ biến bao gồm:
- Gửi tiết kiệm ngân hàng: Là hình thức đầu tư phổ biến, phù hợp với những người tiết kiệm để chi tiêu trong ngắn hạn và trung hạn.
- Tích trữ vàng và ngoại tệ: Mua vàng và ngoại tệ để tích trữ, đến khi nào thấy giá thị trường cao thì bán ra để lấy lãi. Hình thức đầu tư này cũng có những rủi ro như mất cắp, hụt giá.
- Đầu tư bất động sản: Đây là hình thức đầu tư có khả năng sinh lời cao, tuy nhiên cần số vốn đầu tư lớn, kinh nghiệm và thời gian “theo đuổi” trong dài hạn.
- Đầu tư chứng khoán: Đây là kênh đầu tư có tính thanh khoản cao, không đòi hỏi vốn lớn, nhưng đòi hỏi phải có thời gian và kiến thức chuyên môn nhất định, đặc biệt là sự nhạy bén trước khi quyết định đầu tư.
Hiện nay, bên cạnh hình thức tự đầu tư, hình thức đầu tư qua các quỹ đầu tư chuyên nghiệp cũng là xu hướng được nhiều nhà đầu tư cá nhân lựa chọn. Theo đó, tiền đầu tư của nhà đầu tư được gộp chung với các nhà đầu tư khác và được quản lí bởi những chuyên gia tài chính chuyên nghiệp. Các chuyên gia sẽ thay mặt nhà đầu tư để mua – bán và kiểm soát tính rủi ro của các khoản đầu tư.
Trang 61
2. GIẢI QUYẾT MỘT SỐ VẤN ĐỀ VỀ ĐẦU TƯ
Hình thức lãi kép thường được áp dụng cho các khoản đầu tư trong khoảng thời gian trung hoặc dài hạn. Những vấn đề cần chú ý khi đầu tư là: xác định lãi suất đầu tư, xác định thời gian đầu tư và xác định số tiền hiện tại cần đầu tư để nhận được số tiền mong muốn sau một khoảng thời gian đầu tư nhất định.
a) Xác định lãi suất của một khoản đầu tư
Để tìm lãi suất hằng năm r cần thiết để từ khoản tiền vốn ban đầu P ta nhận được số tiền A theo hình thức lãi kép theo định kì với n kì trong một năm, sau N kì hạn, ta cần tìm r từ hệ thức sau
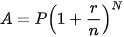
Từ hệ thức này ta suy ra 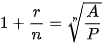 hay
hay
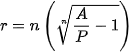 |
Ví dụ 1. Lãi suất năm của khoản đầu tư theo thể thức lãi kép và được tính lãi hằng năm phải là bao nhiêu, nếu bạn muốn tăng gấp đôi khoản đầu tư của mình trong vòng 5 năm?
Giải
Gọi P là số tiền vốn ban đầu. Ta có: A = 2P; n = 1; N = 5.
Do đó để tăng gấp đôi khoản đầu tư trong vòng 5 năm thì lãi suất năm của khoản đầu tư phải là
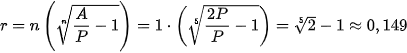 = 14,9%.
= 14,9%.
Luyện tập 1. Lãi suất năm của khoản đầu tư theo thể thức lãi kép và được tính lãi hằng quý phải là bao nhiêu, nếu bạn muốn tăng gấp đôi khoản đầu tư của mình trong vòng 5 năm?
b) Xác định thời gian cho một khoản đầu tư
Để tính số kì gửi N cần thiết cho một khoản đầu tư theo thể thức lãi kép theo định kì với số tiền vốn P, lãi suất năm r, n kì tính lãi trong một năm để đạt được số tiền mong muốn A, ta cần tìm N từ hệ thức sau
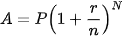 hay
hay 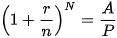 .
.
Lấy lôgarit cơ số 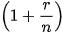 cả hai vế, ta được
cả hai vế, ta được
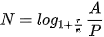 |
Vì vế phải có thể không nguyên, nên thực tế ta sẽ phải chọn N là số tự nhiên nhỏ nhất lớn hơn hay bằng vế phải.
Trang 62
Ví dụ 2. Sẽ mất bao lâu để một khoản đầu tư tăng gấp đôi giá trị nếu nó được tính theo thể thức lãi kép theo định kì và tính lãi hằng năm, với lãi suất 10% mỗi năm?
Giải
Gọi P là số tiền vốn ban đầu. Ta có: A = 2P; n = 1; r = 10% = 0,1.
Khi đầu tư theo thể thức lãi kép theo định kì và tính lãi hằng năm với lãi suất 10% mỗi năm, thì thời gian đầu tư cần thiết là:
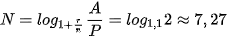 .
.
Vì N phải là số tự nhiên nên ta chọn N = 8. Vậy sau 8 năm thì khoản đầu tư đó sẽ tăng gấp đôi giá trị.
Luyện tập 2. Thực hiện yêu cầu như trong Ví dụ 2, nếu đầu tư theo thể thức lãi kép theo định kì và tính lãi hằng tháng, với lãi suất 10% mỗi năm.
Ví dụ 3. Bác An gửi tiết kiệm 100 triệu đồng theo thể thức lãi kép kì hạn 6 tháng với lãi suất không đổi 8% một năm. Hỏi:
a) Lãi suất đơn hằng năm của khoản gửi tiết kiệm này là bao nhiêu?
b) Sau bao lâu gửi tiết kiệm, bác An nhận được số tiền ít nhất là 150 triệu đồng?
Giải
a) Số tiền bác An nhận được sau 1 năm gửi tiết kiệm là:
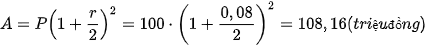 .
.
Số tiền lãi là I = A - P = 108,16 – 100 = 8,16 (triệu đồng).
Vậy lãi suất đơn hằng năm của khoản gửi tiết kiệm này là
![]()
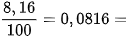 8,16%.
8,16%.
b) Gọi N là số kì hạn gửi tiết kiệm cần thiết, ta có:
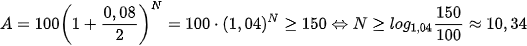 .
.
Vì N là phải số tự nhiên nên ta có N = 11.
Vậy sau 11 kì gửi tiết kiệm, tức là sau 5 năm 6 tháng, bác An sẽ nhận được số tiền ít nhất là 150 triệu đồng.
Luyện tập 3. Vào ngày 1 tháng 1 năm 2020, bác An gửi 200 triệu đồng vào một Tài khoản Hưu trí cá nhân được trả lãi kép kì hạn 12 tháng với lãi suất 5% mỗi năm.
a) Tài khoản này sẽ có giá trị bằng bao nhiêu vào ngày 1 tháng 1 năm 2030?
b) Lãi suất đơn hằng năm của khoản gửi này là bao nhiêu?
Trang 63
c) Xác định giá trị hiện tại của một khoản tiền
Khi nói đến “giá trị thời gian của tiền", ta thường đề cập đến giá trị hiện tại của tiền. Giá trị hiện tại của số tiền A sẽ nhận được vào một ngày nào đó trong tương lai là số tiền vốn P mà bạn cần đầu tư ngay bây giờ để nó sẽ tăng lên thành số tiền A trong khoảng thời gian được chỉ định.
HĐ1. Xây dựng công thức tính giá trị hiện tại của một khoản tiền
Sử dụng công thức lãi kép, hãy tính số tiền vốn P phải gửi theo thể thức lãi kép theo định kì với lãi suất năm r và n kì tính lãi trong một năm để sau t năm gửi sẽ nhận được số tiền mong muốn là A.
Công thức giá trị hiện tại
Giá trị hiện tại P của khoản tiền A sẽ nhận được sau t năm, khi gửi theo thể thức lãi kép theo định kì với n kì tính lãi trong một năm và lãi suất hằng năm r, được tính như sau: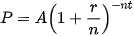 . . |
Chú ý. Giá trị hiện tại của số tiền nhận được trong tương lai luôn nhỏ hơn số tiền sẽ nhận được, vì số tiền nhận được sẽ bằng giá trị hiện tại (tiền đầu tư ngay bây giờ) cộng với tiền lãi tích luỹ được trong khoảng thời gian đó.
Ví dụ 4. Cần đầu tư bao nhiêu tiền bây giờ ở mức lãi suất 6% mỗi năm để sau hai năm nhận được số tiền là 100 triệu đồng, khi việc tính lãi kép được thực hiện:
a) Hằng năm?
b) Hằng tháng?
c) Hằng ngày?
Giải
Ta có: A = 100 (triệu đồng); r = 6% = 0,06; t = 2 (năm).
a) Khi việc tính lãi kép được thực hiện hằng năm (n = 1) thì số tiền cần đầu tư là
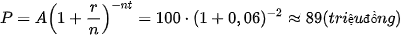 .
.
b) Khi việc tính lãi kép được thực hiện hằng tháng (n = 12) thì số tiền cần đầu tư là
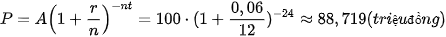 .
.
c) Khi việc tính lãi kép được thực hiện hằng ngày (n = 365) thì số tiền cần đầu tư là
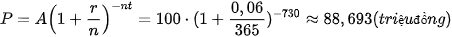 .
.
Trang 64
Luyện tập 4. Một trái phiếu không có phiếu giảm giá có thể được mua lại trong 10 năm tới với giá 100 triệu đồng. Ngay bây giờ, bạn cần bỏ ra bao nhiêu tiền để mua nó nếu bạn muốn nhận lãi kép 6% một năm, tính lãi hằng tháng?
3. LẬP KẾ HOẠCH TÀI CHÍNH CÁ NHÂN
Trong môn Giáo dục kinh tế và pháp luật ở lớp 10, các em đã được học những kiến thức cơ bản về Lập kế hoạch tài chính cá nhân, bao gỏm: khái niệm kế hoạch tải chính cá nhân, các loại tài chính kế hoạch cá nhân (ngắn hạn, trung hạn, dài hạn); tầm quan trọng của việc lập kế hoạch tài chính cá nhân và các bước lập kế hoạch tài chính cá nhân.
Việc lập và thực hiện kế hoạch tài chính cá nhân tốt sẽ giúp chúng ta chủ động cân đối được giữa thu nhập và chi tiêu, tiết kiệm: dành được những khoản chỉ phí cần thiết cho đời sống, học tập; chủ động nắm chắc tình hình tài chính của bản thân để điều chỉnh cho phù hợp; chi tiêu tài chính hợp lí, lành mạnh, không lãng phí, không bị thâm hụt hay nợ nần; hơn nữa, còn tiết kiệm để thực hiện các mục tiêu tài chính quan trọng trong tương lai và giúp tự chủ cuộc sống.
Để lập được kế hoạch tài chính cá nhân và thực hiện thành công kế hoạch này, cần thực hiện các bước cơ bản sau:
- Bước 1: Xác định mục tiêu tài chính và thời hạn thực hiện;
- Bước 2: Theo dõi và kiểm soát thu chỉ cá nhân,
- Bước 3: Thiết lập quy tắc thu chỉ cá nhân;
- Bước 4: Tuân thủ kế hoạch tài chính cá nhân.
Ví dụ 5. Bạn Quỳnh học ở một trường trung học phổ thông xa nhà và phải ở trọ gần trường. Mỗi tháng bố mẹ cho bạn ấy tổng cộng 5 triệu đồng để trang trải các chi phí học tập và sinh hoạt. Em hãy thử lập một kế hoạch tài chính cá nhân để giúp bạn Quỳnh có thể cân đối các khoản chỉ tiêu trong tháng.
Giải
Ta lập kế hoạch cá nhân theo các bước đã nói ở trên:
• Bước 1: Xác định mục tiêu tài chính và thời hạn thực hiện
Ở đây, bạn Quỳnh cần cân đối được số tiền có hằng tháng và các khoản chỉ tiêu hằng tháng, để có kế hoạch chỉ tiêu hợp lí, lành mạnh, không lãng phí, tránh thâm hụt và nợ nần. Thời gian thực hiện kế hoạch của bạn là trong suốt 3 năm học trung học phổ thông.
• Bước 2: Theo dõi và kiểm soát thu chi cá nhân.
Bạn Quỳnh cần xác định rõ các nguồn thu và các khoản chỉ hằng tháng, xác định rõ khoản chi nào là thiết yếu, khoản chi nào có thể tiết kiệm. Cụ thể:
- Các nguồn thu:
+ Tiền được bố mẹ cho hằng tháng: 5 triệu đồng = 5 000 nghìn đồng.
+ Ngoài ra, bạn Quỳnh có thể có một số nguồn thu (không thường xuyên) khác như: tiền thưởng nếu được học sinh giỏi ở cuối kì, tiền giúp việc cho bác chủ nhà trọ khi rãnh
- Các khoản chi:
+ Đóng học phí: 300 nghìn đồng/tháng.
+ Tiền thuê nhà, chi phí điện, nước, cước điện thoại, internet (ở chung với bạn): khoảng 1 100 nghìn đồng/tháng;
Trang 65
+ Tiền ăn uống hằng tháng: khoảng 80 nghìn đồng/ngày x 30 ngày = 2 400 nghìn đồng,
+ Tiền mua các vật dụng thiết yếu, tài liệu, dụng cụ học tập: Khoảng 200 nghìn đồng/tháng,
+ Tiền tiêu vặt, tiền phục vụ nhu cầu giải trí cá nhân (xem phim, mua sách, truyện, ...), đi sinh nhật bạn, đóng quỹ lớp,... đây là những khoản chỉ phát sinh.
• Bước 3: Thiết lập quy tắc thu chi cá nhân
Để có thể cân đối được các khoản thu - chi và có tiền tiết kiệm, đề phòng những trường hợp đột xuất, bạn Quỳnh có thể áp dụng quy tắc: 80/10/10, ở đó:
+ Các khoản chi thiết yếu (học phí, tiền ăn, tiền thuê nhà, tiền điện, nước, ...): chiếm 80% nguồn thu;
+ Các khoản chi phát sinh (sinh nhật, đóng quỹ lớp, giải trí, ..): chiếm 10% nguồn thu;
+ Tiền tiết kiệm: chiếm 10% nguồn thu.
• Bước 4: Tuân thủ kế hoạch tài chính cá nhân.
Để thực hiện thành công kế hoạch tài chính cá nhân đã lập, bạn Quỳnh cần kiên trì tuân thủ theo đúng kế hoạch đã đề ra. Nếu có khoản chi đột xuất ngoài dự kiến thì phải cắt
giảm các khoản chi không thật cần thiết để tránh bị thâm hụt hay nợ nần, và có thể thu xếp thời gian rảnh giúp việc cho bác chủ nhà nhằm tăng thêm khoản thu không thường xuyên để bù lại. Nếu nhu cầu thực tế có thay đổi thì lại cập nhật và điều chỉnh bản kế hoạch cho phù hợp.
Khi lập kế hoạch tài chính cá nhân cho các nhu cầu dài hạn như giáo dục hoặc sống tự lập, bên cạnh việc quản lí tài chính cá nhân thông qua việc phân bổ cân đối nguồn tài chính cá nhân cho các nhu cầu hiện tại, một vấn đề quan trọng là cần có kế hoạch để tích luỹ được số tiền cần thiết thông qua gửi tiết kiệm tích luỹ hoặc đầu tư.
Ta nhắc lại một số kiến thức về niên kim trong SGK Toán 11, tập 1 (bộ sách Kết nối tri thức với cuộc sống)
• Niên kim là một dãy các khoản tiền bằng nhau được gửi định kì. Các khoản tiền gửi định kì có thể là hằng năm, nửa năm, hằng quý, hằng tháng hoặc bất kì khoảng thời gian cố định nào khác. Ví dụ về niên kim là tiền gửi thường xuyên vào tài khoản tiết kiệm tích luỹ, tiền thanh toán hằng tháng khi vay mua nhà trả góp, tiền thanh toán định kì khi mua bảo hiểm nhân thọ,...
• Số tiền của niên kim là tổng của tất cả các khoản tiền gửi được thực hiện và tất cả các khoản tiền lãi tích lũy.
Giả sử P là khoản tiền gửi được thực hiện vào cuối mỗi kì thanh toán cho một niên kim trả lãi suất i trong mỗi kì thanh toán. Số tiền A của niên kim sau n lần gửi tiền là
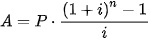 .
.
• Giá trị hiện tại của niên kim là tổng các giá trị hiện tại của các khoản rút.
Giả sử một niên kim có lãi suất i trong mỗi kì thanh toán. Nếu mỗi kì thanh toán rút P đồng và được thực hiện trong n kì, thì giá trị hiện tại V của niên kim là
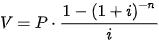 .
.
Trang 66
Nhận xét. Để thực hiện những dự định lớn trong tương lai như tiết kiệm tiền để học đại học, mua nhà, mua xe, đi du lịch, hay tiết kiệm tiền chuẩn bị cho khi nghỉ hưu,... chúng ta cần lập kế hoạch để tích luỹ được số tiền cằn thiết. Ta có thể sử dụng công thức tính niên kim hoặc các hệ thức truy hồi để tính số tiền mà ta sẽ tích luỹ được sau một khoảng thời gian hoặc ước lượng khoảng thời gian cần thiết để tích luỹ đủ số tiền cần thiết, nếu mỗi kì gửi ta có thể gửi đều đặn một số tiền cố định nào đó.
Ví dụ 6. Để tiết kiệm tiền cho việc học đại học sau này của con gái, cô Lan quyết định gửi 1 triệu đồng mỗi tháng vào một tài khoản tích luỹ được ngân hàng đảm bảo lãi suất và trả lãi kép 0,5% hằng tháng. Cô bắt đầu chương trình tiết kiệm này khi con gái cô tròn 3 tuổi. Cô Lan sẽ tiết kiệm được bao nhiêu tiền vào thời điểm gửi khoản tiền lần thứ 180? Lúc này con gái cô bao nhiêu tuổi?
Giải
Ta sử dụng công thức tính số tiền của một niên kim. Ta có:
P = 1 (triệu đồng); l = 0,5% = 0,005; n = 180.
Số tiền mà cô Lan tích luỹ được khi gửi khoản tiền lần thứ 180 là
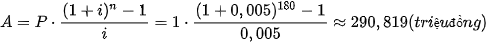 .
.
Mỗi năm có 12 kì gửi tiền, nên thời gian để gửi khoản tiền lần thứ 180 là 180 : 12 = 15 (năm).
Vì cô Lan bắt đầu gửi tiết kiệm tích luỹ khi con gái cô được 3 tuổi, nên khi cô gửi khoản tiền lần thứ 180 thì con gái cô 18 tuổi.
Luyện tập 5. Để tiết kiệm tiền cho việc nghỉ hưu, anh Nam 35 tuổi, quyết định gửi 36 triệu đồng mỗi năm vào Tài khoản Hưu trí Cá nhân trong vòng 30 năm tới. Giá trị của tài khoản sẽ là bao nhiêu khi anh Nam gửi tiền lần thứ 30? Giả sử lãi suất của tài khoản là 6% mỗi năm, được tính lãi kép hằng năm
Ví dụ 7. Chị Hương cân 6 triệu đồng mỗi tháng trong 10 tháng tiếp theo để trang trải các chi phí sinh hoạt trong 1 năm khi học ở trường đại học. Nếu một quỹ thị trường tiền tệ trả lãi kép 0,75% hằng tháng thì bây giờ chị Hương phải xin bố mẹ bao nhiêu tiền gửi vào quỹ đó, để có thể rút ra 5 triệu đồng mỗi tháng trong 10 tháng tiếp theo?
Ta có: P = 5 (triệu đồng); n = 10; i = 0,76% = 0,0075.
Số tiền chị Hương cần gửi vào quỹ thị trường tiền tệ tại thời điểm bây giờ là
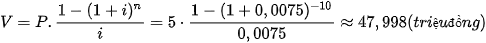
Luyện tập 6. Giải quyết bài toán ở Tình huống mở đầu.
Trang 67
Ví dụ 8. Mất bao lâu để tiết kiệm được 200 triệu đồng nếu mỗi tháng bạn gửi 5 triệu đồng vào một tài khoản tiết kiệm tích luỹ được tính lãi kép hằng tháng, với lãi suất năm là 6%?
Giải
Ta có: A = 200 (triệu đồng); P = 5 (triệu đồng); ![]() .
.
Từ công thức 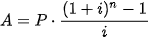 suy ra
suy ra 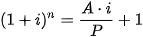 tức là
tức là 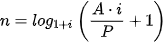 .
.
Do đó số kì gửi cần thiết sẽ là
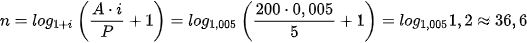 .
.
Vậy số kì cần gửi là 37 kì, tức là sau 3 năm 1 tháng.
Ví dụ 9. Một chuyến đi trải nghiệm thực tế trong kì nghỉ hè sẽ tiêu tốn 4,6 triệu đồng và sẽ phải nộp vào ngày 2/7, trước chuyến đi. Để tiết kiệm tiền cho chuyến đi, vào ngày 1/1 cùng năm, bạn Nam gửi 1 triệu đồng vào một tài khoản tiết kiệm được trả lãi 6% mỗi năm và tính lãi hằng tháng. Bắt đầu từ ngày 1/2, vào ngày đầu tiên của mỗi tháng, bạn Nam gửi đều đặn số tiền 500 nghìn đồng vào tài khoản này.
a) Tìm hệ thức truy hồi biểu thị số tiền trong tài khoản sau n tháng.
b) Tính lần lượt số tiền có trong tài khoản trong 6 tháng đầu tiên (kết quả tính bằng triệu đồng và làm tròn đến chữ số thập phân thứ ba),
c) Sau khi khoản tiền gửi vào ngày 1/7 được thực hiện, tài khoản của bạn Nam có đủ tiền để thanh toán cho chuyến đi trải nghiệm thực tế không?
d) Nếu bạn Nam gửi 600 nghìn đồng mỗi tháng, kể từ ngày 1/2, thì tài khoản của bạn ấy có đủ tiền cho chuyến đi không?
Giải
a) Gọi 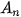 là số tiền (triệu đồng) trong tài khoản của bạn Nam sau n tháng, kể từ ngày 1/1.
là số tiền (triệu đồng) trong tài khoản của bạn Nam sau n tháng, kể từ ngày 1/1.
Ta có hệ thức truy hồi
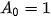 ;
; 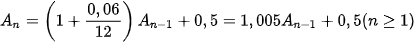 .
.
b) Ta có:
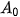 =1 (triệu đồng),
=1 (triệu đồng),
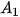 = 1,005
= 1,005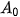 + 0,5 = 1,005 · 1 + 0,5 = 1,505 (triệu đồng);
+ 0,5 = 1,005 · 1 + 0,5 = 1,505 (triệu đồng);
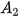 =1,005
=1,005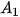 + 0,5 = 1,005 · 1505 + 0,5 ≈ 2,013 (triệu đồng);
+ 0,5 = 1,005 · 1505 + 0,5 ≈ 2,013 (triệu đồng);
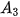 = 1,005
= 1,005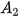 + 0,5 = 1,005 · 2,013 + 0,5 ≈ 2,523 (triệu đồng),
+ 0,5 = 1,005 · 2,013 + 0,5 ≈ 2,523 (triệu đồng),
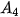 = 1,005
= 1,005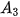 + 0,5 = 1,005 · 2,523 + 0,5 ≈ 3,035 (triệu đồng);
+ 0,5 = 1,005 · 2,523 + 0,5 ≈ 3,035 (triệu đồng);
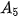 = 1,005
= 1,005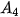 + 0,5 = 1,005 · 3,035 + 0,5 ≈ 3,550 (triệu đồng),
+ 0,5 = 1,005 · 3,035 + 0,5 ≈ 3,550 (triệu đồng),
c) Số tiền trong tài khoản của bạn Nam sau khoản tiên gửi vào ngày 1/7 là
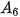 = 1,005
= 1,005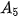 + 0,5 = 1,005 · 3,650 + 0,5 ≈ 4,068 (triệu đồng)
+ 0,5 = 1,005 · 3,650 + 0,5 ≈ 4,068 (triệu đồng)
Như vậy, tài khoản của bạn Nam sẽ không đủ tiền để thanh toán cho chuyến đi trải nghiệm thực tế.
Trang 68
d) Nếu bạn Nam gửi 600 nghìn đồng mỗi tháng, kể từ ngày 1/2, thì hệ thức truy hồi biểu thị số tài khoản của bạn Nam sau n tháng là
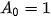 ;
; 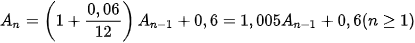 .
.
Trong trường hợp này, tính lần lượt tương tự phần b, ta được 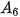 ≈ 4,676 (triệu đồng).
≈ 4,676 (triệu đồng).
Vậy trong trường hợp này, tài khoản của bạn Nam đủ thanh toán cho chuyền đi.
Chú ý. Có thể sử dụng bảng tính Excel hoặc máy tính cằm tay để tính lần lượt các số hạng của một dãy số cho bằng hệ thức truy hồi. Xem chi tiết trong phần Em có biết? ở cuối bài
học này.
Luyện tập 7. Ngày 1/1/2021, bác Hùng quyết định gửi 6 triệu đồng vào cuối mỗi quý vào một Tài khoản Hưu trí Cá nhân.
a) Tìm hệ thức truy hồi biểu thị số dư tài khoản của bác Hùng vào cuối mỗi quý nếu lãi suất được giả định là 8% mỗi năm và được tính lãi hằng quý.
b) Sẽ mất bao lâu trước khi giá trị của tài khoản vượt quá 500 triệu đồng?
c) Giá trị của tài khoản sẽ là bao nhiêu sau 25 năm nữa, khi bác Hùng nghỉ hưu?
BÀI TẬP
3.13. Một trái phiấu không có phiấu giảm giá có thể được mua lại trong 5 năm tới với giá 100 triệu đồng. Ngay bây giờ, bạn cần bỏ ra bao nhiêu tiền để mua nó nếu bạn muốn nhận 1% lãi kép hằng tháng?
3.14. Anh Hưng đầu tư 50 triệu đồng mỗi năm vào một quỹ đầu tư trong vòng 15 năm. Nếu giá trị thị trường của quỹ tăng 5% mỗi năm, thì giá trị tài khoản của anh Hưng sau 15 lần gửi tiền sẽ là bao nhiêu?
3.15. Sẽ mất bao nhiêu năm để tiết kiệm được 100 triệu đồng nếu mỗi tháng bạn gửi 1 triệu đồng vào một tài khoản tích luỹ với lãi suất 6% một năm và được tính lãi kép hằng tháng?
3.16. Tìm giá trị hiện tại của một niên kim mà khoản tiền rút sẽ là 5 triệu đồng mỗi tháng trong vòng 48 tháng với lãi suất năm là 6%.
3.17. Anh Dương đi làm thêm trong mùa hè để kiếm tiền giúp trang trải chi phí học tập ở trường đại học vào năm sau. Anh Dương có thể tiết kiệm được 1,5 triệu đồng mỗi tuần
trong 12 tuần và anh đầu tư nó với lãi kép 0,4% hằng tuần.
a) Anh Dương có tổng cộng bao nhiêu tiền sau 12 tuần?
b) Khi năm học mới bắt đầu, anh Dương sẽ bắt đầu rút số tiền bằng nhau từ tài khoản này mỗi tuần. Số tiền anh Dương có thể rút nhiều nhất mỗi tuằn trong vòng 36 tuần
là bao nhiêu?
3.18. Anh Nam và chị Hương cần có 2 tỉ đồng để mua một căn nhà sau 4 năm nữa. Hỏi bây giờ họ cần gửi bao nhiêu tiền vào tài khoản tiết kiệm để có thể thực hiện việc này, biết
rằng ngân hàng trả lãi kép 2% hằng quý?
Trang 69
Em có biết?
Tính các số hạng của một dãy số cho bởi hệ thức truy hồi bằng máy tính cầm tay hoặc phần mềm bảng tính Excel.
• Ta có thể sử dụng máy tính cầm tay để tính lần lượt các số hạng của dãy số truy hồi.
Quay lại Ví dụ 9, ta có dãy số truy hồi với: 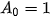 ;
; 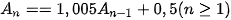 .
.
Để tìm các số hạng của dãy số trên, ta nhập vào máy tính biểu thức:
x = x + 1 : A = 1,005A + 0,5
bằng cách bắm tổ hợp phím sau:
![]()
ở đó, x tương ứng với chỉ số của các số hạng trong dãy (chính là n), A là giá trị của số hạng 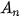 (hay chính là
(hay chính là 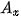 ).
).
Khi đó, màn hình hiển thị: 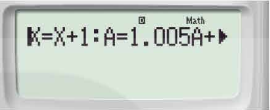
Ta tiếp tục bấm phím ![]() và lần lượt nhập các giá trị x = 0, A = 1, sau đó bấm phím
và lần lượt nhập các giá trị x = 0, A = 1, sau đó bấm phím  , màn hình hiển thị
, màn hình hiển thị 
Tức là 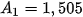 . Tiếp tục bắm phím
. Tiếp tục bắm phím ![]() liên tục, ta thu được
liên tục, ta thu được 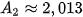 ;
; 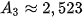 ,...
,...
Vậy để tìm số hạng thứ n, ta bấm phím ![]() cho tới khi x dừng lại ở giá trị n, khi đó ta tìm được giá trị
cho tới khi x dừng lại ở giá trị n, khi đó ta tìm được giá trị 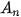 .
.
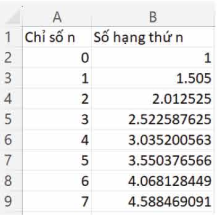
• Bên cạnh việc sử dụng máy tính cầm tay để tính lần lượt các số hạng của dãy số truy hồi, ta có thể sử dụng bảng tính Excel để tính số hạng này như hình bên.
Mở bảng tính Excel, ta lập ra hai cột, một cột là chỉ số n, một cột là giá trị của số hạng thứ n. Ta nhập giá trị đầu tiên của chỉ số n là 0, sau đó đặt con trỏ chuột ở góc dưới bên phải của ô số 0, bấm phím Ctrl, ta thấy xuất hiện biểu tượng dấu cộng và kéo chuột xuống, ta được một dãy số theo thứ tự như hình bên.
Tiếp tục, ta nhập giá trị đầu tiên của dãy số 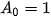 , ở ô B2. Tại ô B3, ta nhập =1.005*$B2+0.5 (tức là ta lấy 1,005 nhân với kết quả ở ô B2 rồi cộng với 0,5) và nhấn Enter, ta thu được kết quả
, ở ô B2. Tại ô B3, ta nhập =1.005*$B2+0.5 (tức là ta lấy 1,005 nhân với kết quả ở ô B2 rồi cộng với 0,5) và nhấn Enter, ta thu được kết quả 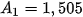 .
.
Ta tiếp tục đặt con trỏ chuột ở góc dưới bên phải của ô B3, bấm phím Ctrl, ta thấy xuất hiện biểu tượng dấu cộng và kéo chuột xuống, ta được các số hạng cần tìm. `
Tức là 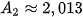 ;
; 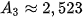 ,...
,...