Trang 46
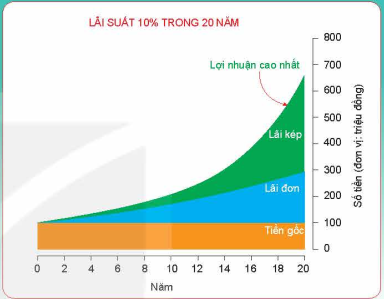
LÃI SUẤT 10% TRONG 20 NĂM
Chuyên đề này giới thiệu những kiến thức cơ bản về tiền tệ, lãi suất, lạm phát, thẻ tín dụng, vay nợ, cũng như cách thức tính lãi suất, các hình thức gửi tiết kiệm, trả các khoản nợ đúng hạn. Qua đó, có thể vận dụng các kiến thức đã học để thiết lập kế hoạch tài chính cá nhân cho các nhu cầu dài hạn cũng như giải quyết một số vấn đề về đầu tư.
| THUẬT NGỮ • Tiền tệ • Lãi đơn • Lãi kép • Lạm phát • Lãi suất thực | KIẾN THỨC, KĨ NĂNG • Nhận biết một số vấn đề về tiền tệ. • Nhận biết một số vấn đề về lãi suất của các tổ chức tín dụng. • Tính lãi suất được hưởng qua tiền tiết kiệm và các giá trị thực chất có tính đến lạm phát. • Vận dụng kiến thức toán học trong việc giải quyết một số vấn để về lãi suất của các tổ chức tín dụng. |
Bác An có 500 triệu đồng muốn gửi vào ngân hàng trong thời hạn 9 tháng để lấy lãi. Bác đang phân vân giữa hai phương án như sau:
- Phương án 1: Tiền gửi tính theo lãi đơn, với lãi suất năm là 6,1%,
- Phương án 2: Tiền gửi tính theo lãi kép kì hạn 1 tháng, với lãi suất năm là 6%.
Hình thức gửi tiền nào có lợi hơn cho bác An?
Trang 47
1. KHÁI NIỆM TIỀN TỆ
(Nguồn: N. Gregory Mankiw, Macroeconomics, 8th edition, Worth Publishers, 2012).
a) Khái niệm tiền tệ
Tiền tệ là một phương tiện thanh toán chính quy theo pháp luật, được sử dụng với mục đích trao đổi hàng hoá, dịch vụ của một khu vực, quốc gia hay một nền kinh tế. Vì vậy, tiền tệ còn được gọi là “tiền lưu thông”.
Thông thường, tiền tệ được phát hành bởi cơ quan nhà nước (như ngân hàng trung ương). Bản thân tiền tệ thực ra không có giá trị. Giá trị của nó phụ thuộc vào giá trị mà nó đại diện, tuỳ theo nền kinh tế và nhà phát hành. Giá cả của tiền tệ chính là lãi suất, nói một cách khác, giá cả của tiền tệ là số tiền mà người ta phải trả cho cơ hội được vay nó trong một khoảng thời gian xác định.
Khi phân biệt tiền tệ của quốc gia này với tiền tệ của quốc gia khác, người ta dùng cụm từ “đơn vị tiền tệ”. Đơn vị tiền tệ của nhiều quốc gia có thể có cùng tên gọi và để phân biệt chúng, người ta thường phải gọi kèm tên quốc gia sử dụng đồng tiền, ví dụ đô la Mỹ, đô la Úc, đô la Singapore...
Câu hỏi
Hãy kể tên các mệnh giá thường gặp của tờ tiền đồng Việt Nam.
b) Chức năng của tiền tệ
Tiền tệ có ba chức năng cơ bản:
- Là phương tiện đo lường giá trị: Tiền tệ là phương tiện để đo lường giá trị của hàng hoá, dịch vụ. Mỗi hàng hoá sẽ được định giá trị bằng tiền tệ, nó tương tự như cách chúng ta định khối lượng bằng cân hay định chiều dài bằng mét. Giá trị của hàng hoá khi được biểu hiện bằng tiền tệ gọi là giá cả. Giá cả này lại chịu ảnh hưởng từ nhiều nhân tố khác như giá trị hàng hoá, giá trị của tiền tệ và quan hệ cung-cầu trên thị trường.
- Là phương tiện trao đổi, thanh toán: Tiền tệ làm đơn giản hoá quá trình trao đổi hàng hoá, dịch vụ giữa các chủ thể. Tiền có thể được dùng để giao dịch mua bán, trả nợ, nộp thuế.... Tiền tệ được công nhận và có độ chính xác cao về giá trị trao đổi. Tiền tệ đóng vai trò là vật trung gian, vật ngang giá chung. Tiền tệ là phương tiện giúp cho hoạt động mua bán được diễn ra thuận tiện và
nhanh chóng.
- Là phương tiện tích luỹ tài sản: Vì có thể dễ dàng đổi tiền lấy các hàng hoá cần thiết vào thời điểm cần thiết, nên giữ tiền là một hình thức tích trữ tài sản để dùng trong tương lai. Tiền tệ được xem là tài sản tích luỹ khi tiền được rút khỏi hoạt động lưu thông trên thị trường và đem đi cất trữ. Lượng tiền cất trữ càng nhiều thì của cải vật chất trong xã hội càng lớn.
Hình thức trao đổi trực tiếp hàng hoá khi chưa xuất hiện tiền tệ (tranh minh hoạ)
Trang 48
c) Tính chất của tiền tệ
Để có thể thực hiện được các chức năng của tiền, tiền tệ phải có những tính chất cơ bản sau đây:
- Dễ bảo quản, dễ vận chuyển, dễ chia nhỏ để tiện lợi cho việc tích trữ tài sản và trao đổi hàng hoá.
- Tính đồng nhất: Dù là tiền bằng chất liệu gì, phát hành vào thời điểm nào, nhưng nếu có tổng mệnh giá như nhau theo cùng một đơn vị tiền nào đó thì có giá trị bằng nhau.
- Được tin tưởng và chấp nhận: Mọi người chấp nhận là tiền có giá trị, sẵn sàng đổi hàng hoá của mình lấy tiền. Để được tin tưởng và chấp nhận, tiền phải có được giá trị ổn định, lượng cung hạn chế và khó làm giả.
d) Nguyên tắc tổng tiền bằng 0
Mọi khoản tiền dương mà một tổ chức hay cá nhân nào đó đang có đều ứng với khoản nợ mà những tổ chức, cá nhân khác nợ người này, và ngược lại mọi khoản tiền âm của ai đó đều ứng với những khoản tiền dương mà những người khác cho người đó vay. Tổng quát: Tổng tiền pháp định (tức là đồng tiền được phát hành chính thức bởi cơ quan nhà nước), kể cả các khoản dương (cho vay) và khoản âm (vay), là bằng 0. Đây gọi là nguyên tắc tổng tiền bằng 0.
Nguyên tắc tổng tiền bằng 0 cho ta thấy một điều rất rõ là: tổng cộng giá trị của tất cả các tài sản trên thế giới chính là do giá trị của các tài sản (ngoài tiền) tạo thành, chứ không phải do giá trị của tiền tạo thành. Tiền chỉ có tác dụng làm thước đo của tài sản và làm công cụ giao dịch tài sản, thêm tiền pháp định lưu hành trên thế giới không có nghĩa là thế giới có thêm tài sản.
2. LÃI SUẤT VÀ CÁCH TÍNH LÃI SUẤT
Số tiền vay của một cá nhân từ ngân hàng hoặc tổ chức tín dụng dưới hình thức cho vay hay số tiền vay của ngân hàng từ một cá nhân dưới hình thức tài khoản tiết kiệm, được gọi là tiền vốn (hay tiền gốc).
Tiền lãi được hiểu là thu nhập từ một khoản vay bằng tiền tệ. Đây là số tiền mà người đi vay phải trả cho người cho vay, để bù đắp cho lợi ích của việc nắm giữ một lượng tiền trong một khoảng thời gian nhất định.
Lãi suất là tỉ lệ mà theo đó tiền lãi được người vay trả cho việc sử dụng tiền mà họ vay từ người cho vay. Lãi suất thường được thể hiện như là tỉ lệ phần trăm của tiền gốc trong khoảng thời gian một năm.
Có hai hình thức tính lãi thường gặp: Lãi đơn và lãi kép (còn gọi là lãi gộp).
Những lưu ý quan trọng đối với một khoản vay:
– Số tiền cho vay;
– Thời gian cho vay;
– Lãi suất;
– Kì tính lãi;
– Hình thức trả nợ.
Trang 49
a) Lãi đơn
Lãi đơn là phương thức tính lãi mà tiền lãi sau mỗi kì không được nhập vào vốn để tính lãi cho kì sau. Tiền lãi của mỗi kì đều được tính theo vốn gốc ban đầu và đều bằng nhau.
HĐ1. Xây dựng công thức lãi đơn
Giả sử gửi một khoản tiền vốn P vào ngân hàng theo thể thức lãi đơn với lãi suất năm là r (r được cho dưới dạng số thập phân).
a) Tính số tiền lãi l nhận được sau t năm.
b) Số tiền nhận được sau t năm bao gồm số tiền vốn P ban đầu và số tiền lãi I. Hãy tính tổng số tiền A nhận được sau 1 năm.
Ngân hàng thưởng công bố lãi suất năm dưới dạng phần trăm. Lãi suất r = 5% nghĩa là
r = 5% =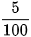 
= 0,05.
Công thức lãi đơn
| • Nếu gửi một khoản tiền vốn P với lãi suất đơn là r mỗi năm trong thời hạn 1 năm, thì số tiền lãi l được nhận là l = Prt. • Số tiền A được nhận sau 1 năm là tổng số tiền vốn P ban đầu và số tiền lãi được nhận, và bằng A = P + I = P(1 + rt). |
Chú ý. Lãi đơn chủ yếu được dùng cho các khoản gửi hoặc đầu tư ngắn hạn (thường là dưới 1 năm). Trong một số trường hợp, thời gian gửi hoặc đầu tư t được tính chính xác theo ngày và người ta thường quy ước một năm tài chính có 365 ngày. Khi đó công thức tính lãi đơn là:
,
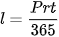ở đó t là số ngày gửi (hoặc đầu tư) thực tế của khoản gửi đó.
Ví dụ 1. Bác An cho một tổ chức tín dụng vay 100 triệu đồng trong thời hạn 9 tháng với lãi suất đơn là 10% mỗi năm. Tính số tiền lãi và tổng số tiền bác An nhận được sau 9 tháng.
Giải
Ở đây ta có:
P = 100 (triệu đồng); r = 10% = 0,1;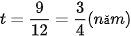 
.
Số tiền lãi bác An nhận được là:
I = Prt = 100 · 0,1 ·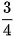 
= 7,5 (triệu đồng).
Tổng số tiền bác An nhận được là:
A = P + I = 100 + 7,5 = 107,5 (triệu đồng).
Luyện tập 1. Anh Hưng cho một tổ chức tín dụng vay 50 triệu đồng trong thời hạn 6 tháng theo thể thức lãi đơn. Lãi suất năm của khoản cho vay này là bao nhiêu nếu số tiền anh Hưng nhận được sau 6 tháng là 52 triệu đồng?
Trang 50
b) Lãi kép
Lãi kép là phương thức tính lãi mà tiền lãi sau mỗi kì được nhập vào tiền vốn để được tiền vốn mới, dùng để tính lãi cho kì tiếp theo.
HĐ2. Xây dựng công thức lãi kép
Giả sử gửi một khoản tiền vốn P vào ngân hàng theo thể thức lãi kép với lãi suất năm là r (r được cho dưới dạng số thập phân), được tính lãi n kì trong một năm.
a) Tính lãi suất của mỗi kì.
b) Tính số tiền nhận được (cả vốn lẫn lãi) sau 1 kì, sau 2 kì.
c) Dự đoán công thức tính số tiền nhận được sau N kì gửi.
Công thức lãi kép
Số tiền A thu được sau t năm do một khoản vốn P được đầu tư theo thể thức lãi kép theo định kì, với lãi suất hằng năm r và được tính lãi n kì mỗi năm, là . |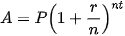
Chú ý. Trong công thức lãi kép, số tiền A thường được gọi là giá trị tương lai và P được gọi là giá trị hiện tại của tài khoản.
Lãi kép thường được sử dụng cho các khoản gửi tiết kiệm hoặc các khoản đầu tư trung và dài hạn.
Ví dụ 2. Một người gửi tiết kiệm 100 triệu đồng theo thể thức lãi kép với lãi suất năm là 9% thì số tiền nhận được sau 3 năm là bao nhiêu nếu việc tính lãi diễn ra:
a) Hằng năm?
b) Hằng quý?
c) Hằng tháng?
Tính số tiền lãi nhận được trong mỗi trường hợp.
Giải
Sử dụng công thức lãi kép, ta có:
P = 100 (triệu đồng); r = 9% = 0,09; t = 3 năm.
a) Khi tính lãi hằng năm thì số kì tính lãi trong một năm là n = 1.
Do đó số tiền nhận được là:
A = P(1 + r)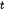
= 100 · (1 + 0,09)
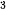≈ 129,503 (triệu đồng).
Số tiền lãi là:
129,503 – 100 = 29,503 (triệu đồng).
b) Khi tính lãi hằng quý thì số kì tính lãi trong một năm là n = 4. Do đó số tiền nhận được là:
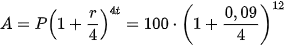≈ 130,605 (triệu đồng).
Số tiền lãi là:
130,605 – 100 = 30,605 (triệu đồng).
Trang 51
c) Khi tính lãi hằng tháng thì số kì tính lãi trong một năm là n = 12. Do đó số tiền nhận được là:
≈ 130,865 (triệu đồng).
Số tiền lãi là:
130,865 – 100 = 30,865 (triệu đồng).
Luyện tập 2. Trở lại Ví dụ 2, hãy tính số tiền nhận được và số tiền lãi tương ứng sau 3 năm gửi tiết kiệm nếu việc tính lãi diễn ra hằng ngày (giả sử một năm có 365 ngày).
Vận dụng. Giải quyết bài toán trong Tình huống mở đầu.
3. LẠM PHÁT
a) Khái niệm lạm phát, tỉ lệ lạm phát
(Nguồn: N. Gregory Mankiw, Macroeconomics, 8th edition, Worth Publishers, 2012).
Lạm phát là sự tăng mức giá chung một cách liên tục của hàng hoá, dịch vụ theo thời gian và là sự mất giá trị của một loại tiền tệ nào đó. Khi mức giá chung tăng cao, một đơn vị tiền tệ sẽ mua được ít hàng hoá và dịch vụ hơn so với trước đây, do đó lạm phát phản ánh sự suy giảm sức mua trên một đơn vị tiền tệ.
Sức mua là số lượng hàng hóa hay dịch vụ có thể mua được bằng 1 đơn vị tiền tệ. Ví dụ, với 100 nghìn đồng vào thời điểm tháng 1/ 2024 có thể mua được hơn 4 lít xăng RON 95,
Tỉ lệ lạm phát là tốc độ tăng mặt bằng giá của nền kinh tế. Nó cho thấy mức độ lạm phát của nền kinh tế. Chẳng hạn, tỉ lệ lạm phát hằng năm là 3% nghĩa là sức mua trị giá 1 triệu đồng bây giờ sẽ chỉ còn sức mua 970 nghìn đồng trong một năm tới vì 3% của 1 triệu đồng ban đầu đã bị xói mòn do lạm phát.
Thông thường, tỉ lệ lạm phát được tính dựa vào chỉ số giá tiêu dùng CPI hoặc chỉ số giảm phát GDP. Tỉ lệ lạm phát có thể được tính cho một tháng, một quý, nửa năm hay một năm.
Tỉ lệ lạm phát là thước đo tỉ lệ giảm xuống sức mua của đồng tiền. Nó là một biến số được sử dụng để tính toán lãi suất thực cũng như điều chỉnh mức lương.
Ví dụ 4. Giả sử tỉ lệ lạm phát trung bình hằng năm là g (biểu thị dưới dạng số thập phân), g < 1. Khi đó sức mua A mà số tiền P (tại thời điểm hiện tại) sẽ mua được sau n năm nữa là
A = P(1 - g)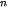
.
(Theo M. Sullivan, Finite Mathematics, 11th edition, Wiley, 2010)
a) Nếu tỉ lệ lạm phát hằng năm là 4%, thì sức mua của 1 triệu đồng là bao nhiêu sau 3 năm nữa?
b) Nếu số tiền 1 triệu đồng chỉ còn sức mua 900 nghìn đồng sau 2 năm, thì tỉ lệ lạm phát trung bình mỗi năm là bao nhiêu phần trăm (làm tròn đến chữ số thập phân thứ nhất) ?
Trang 52
Giải
a) Sức mua của 1 triệu đồng sau 3 năm nữa là:
A = 1 · (1 – 0,04)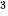
= 0,884736 (triệu đồng).
Vậy sau 3 năm nữa thì sức mua của 1 triệu đồng chỉ còn 884 736 đồng.
b) Ta có: A = 0,9; P = 1; n =2. Do đó, từ công thức A = P(1 − g)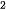
suy ra
.
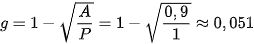Vậy tỉ lệ lạm phát trung bình hằng năm là khoảng 5,1%.
Luyện tập 4. Giả sử tỉ lệ lạm phát trung bình hằng năm là 4%. Sử dụng công thức tính sức mua ở Ví dụ 4, hãy cho biết mất bao nhiêu năm thì sức mua giảm xuống chỉ còn một nửa?
b) Các giá trị thực chất có tính đến lạm phát
Nếu r là lãi suất năm của thị trường (biểu thị dưới dạng số thập phân), 1 đồng đầu tư vào đầu năm sẽ trở thành (1 + r) đồng vào cuối năm.
Tuy nhiên, nếu tỉ lệ lạm phát của nền kinh tế là g, thì sức mua của (1 + r) đồng chỉ là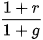 
.
Từ đó, lãi suất thực là
 |
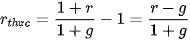Dễ thấy khi g = 0 thì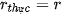 
và lãi suất thực dương nếu lãi suất gửi lớn hơn tỉ lệ lạm phát, lãi suất thực âm nếu lãi suất gửi nhỏ hơn tỉ lệ lạm phát.
Ví dụ 5. Anh Nam gửi tiết kiệm 500 triệu đồng kì hạn 12 tháng, với lãi suất năm là 9%. Giả sử tỉ lệ lạm phát của nền kinh tế năm đó là 4%. Cuối kì hạn gửi, anh Nam rút tiền cả vốn lẫn lãi.
a) Thu nhập thực (tức là số tiền lãi thu được tính theo lãi suất thực, đã tính đến yếu tố lạm phát) cho khoản gửi tiết kiệm của anh Nam là bao nhiêu?
b) Thu nhập thực sau thuế của anh Nam là bao nhiêu, nếu giả sử anh Nam phải nộp thuế thu nhập cá nhân 10%?
Giải
Ta có: P = 500 (triệu đồng); r = 9% = 0,09; g = 4% = 0,04.
a) Lãi suất thực cho khoản gửi tiết kiệm của anh Nam là
.
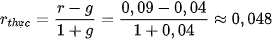Vậy thu nhập thực của anh Nam là
500 · 0,048 = 24 (triệu đồng).
b) Lãi suất thực sau thuế khi chưa tính lạm phát là:
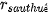= 9% · (100% - 10%) = 8,1% = 0,081.
Do đó thu nhập thực sau khi tính thuế của anh Nam là:
.
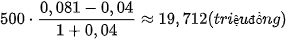Trang 53
Chú ý. Trong trường hợp mà tỉ lệ lạm phát thấp (g nhỏ, ví dụ không quá 5%), người ta coi 1 + g xấp xỉ bằng 1 và thường dùng công thức gần đúng sau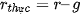 
, tức là lãi suất thực xấp xỉ bằng lãi suất danh nghĩa trừ đi tỉ lệ lạm phát.
Luyện tập 5. Thực hiện các yêu cầu như trong Ví dụ 5, nếu tỉ lệ lạm phát của nền kinh tế năm đó là 7%.
BÀI TẬP
3.1. Tìm lãi suất đơn (tính theo năm), biết số tiền vốn ban đầu là 900 triệu đồng và số tiền lãi thu được trong thời hạn 6 tháng là 54 triệu đồng.
3.2. Tìm thời gian gửi t (tính theo ngày), để 100 triệu đồng tích luỹ được thành 105 triệu đồng với lãi suất đơn là 11% một năm. Ở đây một năm tài chính được lấy là 365 ngày.
3.3. Ngân hàng A đấu giá lô trái phiếu Chính phủ có mệnh giá 100 tỉ đồng, thời hạn 9 tháng với mức giá sẵn lòng trả là 96 tỉ đồng. Giả sử cuộc đấu giá thành công như mong muốn thì ngân hàng A sẽ được hưởng lãi suất bao nhiêu, nếu tính theo hình thức lãi suất đơn.
3.4. Tính số tiền A thu được sau 5 năm nếu số tiền 200 triệu đồng được gửi ngân hàng với lãi suất 9% một năm theo thể thức:
a) Tính lãi kép hằng năm;
b) Tính lãi kép hằng quý.
Tính số tiền lãi tương ứng trong mỗi trường hợp.
3.5. Giả sử tỉ lệ lạm phát của nền kinh tế là 3,5%/năm.
a) Với tỉ lệ lạm phát này, sức mua của 10 triệu đồng ở hiện tại là bao nhiêu sau 1 năm nữa?
b) Một người gửi tiết kiệm 600 triệu đồng ki hạn 12 tháng với lãi suất năm là 8%. Hỏi thu nhập thực của người đó khi rút sổ tiết kiệm sau 1 năm nữa, tức là tiền lãi gửi tiết kiệm sau khi tính theo lãi suất thực đã tính đến yếu tố lạm phát, là bao nhiêu?
3.6. Chỉ số giá tiêu dùng (CPI) cho biết sự thay đổi tương đối về giá theo thời gian của một giỏ hàng hoá và dịch vụ cố định. Nó là một chỉ số giá sinh hoạt giúp đo lường ảnh hưởng của lạm phát đến chi phí hàng hoá và dịch vụ. Nếu lấy chỉ số CPI của kì gốc 2014 để so sánh (coi CPI cho năm này là 100) thì chỉ số CPI tháng 1 năm 2020 là 118,09 (Theo Tổng cục thống kê). Điều này có nghĩa là 100 nghìn đồng trong năm 2014 có sức mua tương đương với 118,09 nghìn đồng vào tháng 1 năm 2020. Nói chung, nếu tỉ lệ lạm phát trung bình là g mỗi năm (g cho dưới dạng số thập phân) trong n năm, thì chỉ số CPI sau n năm là
,
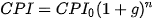ở đó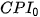 
là CPI tại đầu của chu kì n năm.
a) Chỉ số CPI là 100 vào tháng 1 năm 2014 và 118,09 vào tháng 1 năm 2020. Giả sử rằng tỉ lệ lạm phát hằng năm không đổi trong khoảng thời gian này, hãy xác định tỉ lệ lạm phát trung bình hằng năm trong giai đoạn này.
b) Sử dụng tỉ lệ lạm phát tính được từ câu a, CPI sẽ đạt mức 115 vào năm nào?
c) Nếu CPI tháng 1 năm 2020 là 118,09 và tỉ lệ lạm phát trung bình hằng năm là 3,21% thì CPI vào tháng 1 năm 2030 sẽ là bao nhiêu?
d) Nếu tỉ lệ lạm phát trung bình hằng năm là 3%, thì sẽ mất bao lâu để chỉ số giá tiêu dùng tăng gấp đôi?
