Trang 22
BÀI TẬP CUỐI CHUYÊN ĐỀ 1
1.13. Một chiếc hộp đựng ba tấm thẻ cùng loại ghi số 0, ghi số 1 và ghi số 2. Bạn An rút thẻ ba lần một cách độc lập, mỗi lần rút một tấm thẻ từ trong túi, ghi lại số trên tấm thẻ rồi
trả lại thẻ vào hộp. Gọi X là tổng ba số An nhận được sau ba lần rút thẻ. Lập bảng phân bố xác suất của X.
1.14. Có ba chiếc túi I, II và III. Túi I có chứa 5 viên bị trắng và 6 viên bi đen cùng kích thước, khối lượng. Túi II và III mỗi túi có chứa 2 viên bi trắng và 8 viên bi đen. Bạn Minh lấy
ngẫu nhiên từ mỗi túi một viên bi. Gọi X là số viên bi trắng lấy được.
a) Lập bảng phân bố xác suất của X.
b) Chứng minh rằng X không phải là biến ngẫu nhiên có phân bố nhị thức.
1.15. Một cuộc thi gồm hai loại câu hỏi: Câu hỏi loại 1 và câu hỏi loại 2. Ở vòng 1 thí sinh bốc ngẫu nhiên câu hỏi loại i ∈ {1; 2}. Nếu trả lời sai thì thí sinh dừng cuộc thi tại đây. Nếu trả lời đúng, thí sinh sẽ đi tiếp vào vòng 2, tiếp tục bốc ngẫu nhiên một câu hỏi loại j ∈ {1; 2} (j ≠ i). Sau khi thí sinh trả lời câu hỏi này, cuộc thi kết thúc. Thí sinh sẽ nhận được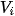 
điểm nếu trả lời đúng câu hỏi loại i ∈ {1; 2}. Giả thiết rằng việc trả lời đúng câu hỏi vòng 1 sẽ không ảnh hưởng đến xác suất trả lời đúng hay sai câu hỏi ở vòng 2.
Bạn An tham gia cuộc thi. Gọi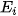 
là biến cố: "An trả lời đúng câu hỏi loại i" (i ∈ {1; 2}). Giả sử P() = 
.
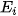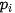a) Với điều kiện nào thì ở vòng 1, An nên bốc ngẫu nhiên câu hỏi loại 1?
b) Giả sử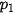 
= 0,6, 
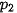= 0,8, 
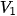=20,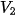 
= 0. Khi đó ở vòng 1, An nên bốc ngẫu nhiên câu hỏi loại nào?
1.16. Hai kì thủ Hoà và Trường thi một trận đấu cờ. Biết rằng thể lệ ở mỗi ván đầu trong trận này không có kết quả hoà. Xác suất thắng của Trường trong một ván là 0,4. Trận đầu gồm 7 ván. Người nào thắng một số ván lớn hơn là người thắng cuộc. Tính xác suất để Trường là người thắng cuộc.
1.17. Một hệ thông tin có n thành phần hoạt động độc lập với nhau. Xác suất hoạt động của mỗi thành phần là p. Hệ hoạt động nếu có ít nhất một nửa các thành phần hoạt động.
Với giá trị nào của p thì hệ 5 thành phân tốt hơn hệ 3 thành phần?
1.18. Một cửa hàng cho thuê xe ô tô tự lái. Chi phí cửa hàng phải tiêu tốn cho một chiếc xe là a triệu đồng/ngày. Mỗi chiếc xe được cho thuê thì cửa hàng thu về được 1 triệu đồng/ngày. Biết rằng nhu cầu cho thuê trong một ngày là một biến ngẫu nhiên rời rạc X có bảng phân bố xác suất như sau:
| X | 0 | 1 | 2 | 3 | 4 |
| P | 0,0608 | 0,1703 | 0,2384 | 0,2225 | 0,308 |
a) Giả sử cửa hàng có 3 chiếc ô tô cho thuê. Gọi Y là số tiền cửa hàng thu được trong 1 ngày. Lập bảng phân bố xác suất của Y. Hỏi trung bình một ngày cửa hàng thu được bao nhiêu tiền từ việc cho thuê xe?
b) Giả sử cửa hàng có 4 chiếc ô tô cho thuê. Gọi Z là số tiền cửa hàng thu được trong 1 ngày. Lập bảng phân bố xác suất của Z. Hỏi trung bình một ngày cửa hàng thu được bao nhiêu tiền từ việc cho thuê xe?
c) Với giá trị nào của a thì cửa hàng chỉ nên duy trì 3 xe ô tô cho thuê?
